4장. 기본 신경망 구현

해당 포스트는 책 “골빈해커의 3분 딥러닝 텐서플로맛”의 4장 “기본 신경망 구현”을 학습하고 내용을 정리한 글입니다.

• 기본적인 신경망 모델, 딥러닝인 심층 신경망, 즉 다층 신경망을 간단하게 구현
• 그에 앞서 딥러닝 구현에 꼭 필요한 기초 개념 확인

4.1 인공신경망의 작동 원리

4.1.1 인공신경망(artificial neural network) 의 개념

• 뇌를 구성하는 신경 세포, 즉 뉴런(neuron) 의 동작 원리에 기초

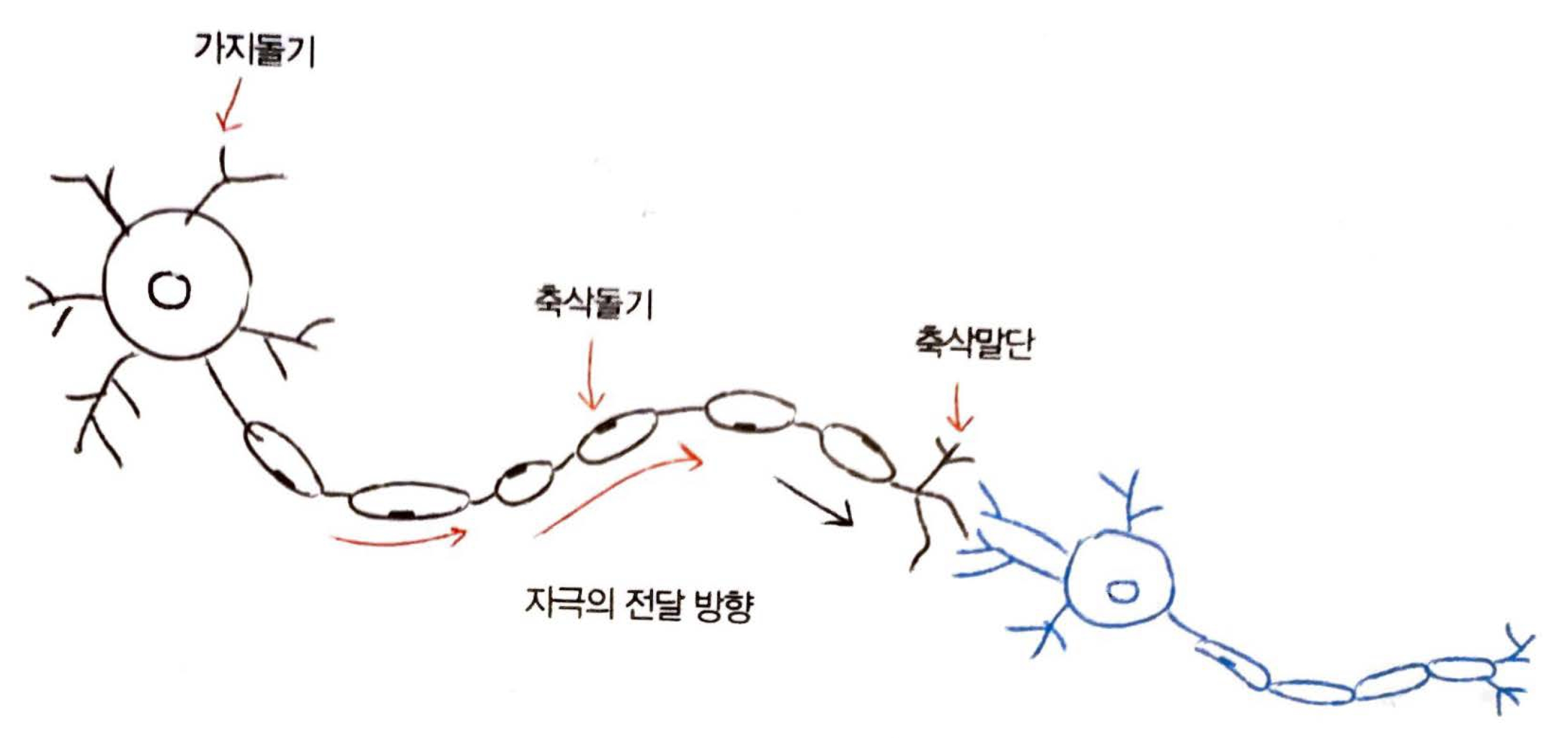
뉴런의 기본 동작

• 가지돌기에서 신호를 받아들임
• 신호가 축삭돌기를 지나 축삭말단으로 전달됨
• 축삭돌기를 지나는 동안 신호가 약해지거나, 너무 약해서 축삭말단까지 전달되지 않거나, 또는 강하게 전달되기도 함
• 축삭말단까지 전달된 신호는 연결된 다음 뉴런의 가지돌기로 전달됨
• 수억 개의 뉴런 조합을 통해 손가락을 움직이거나 물체를 판별하는 등 다양한 조작과 판단을 수행

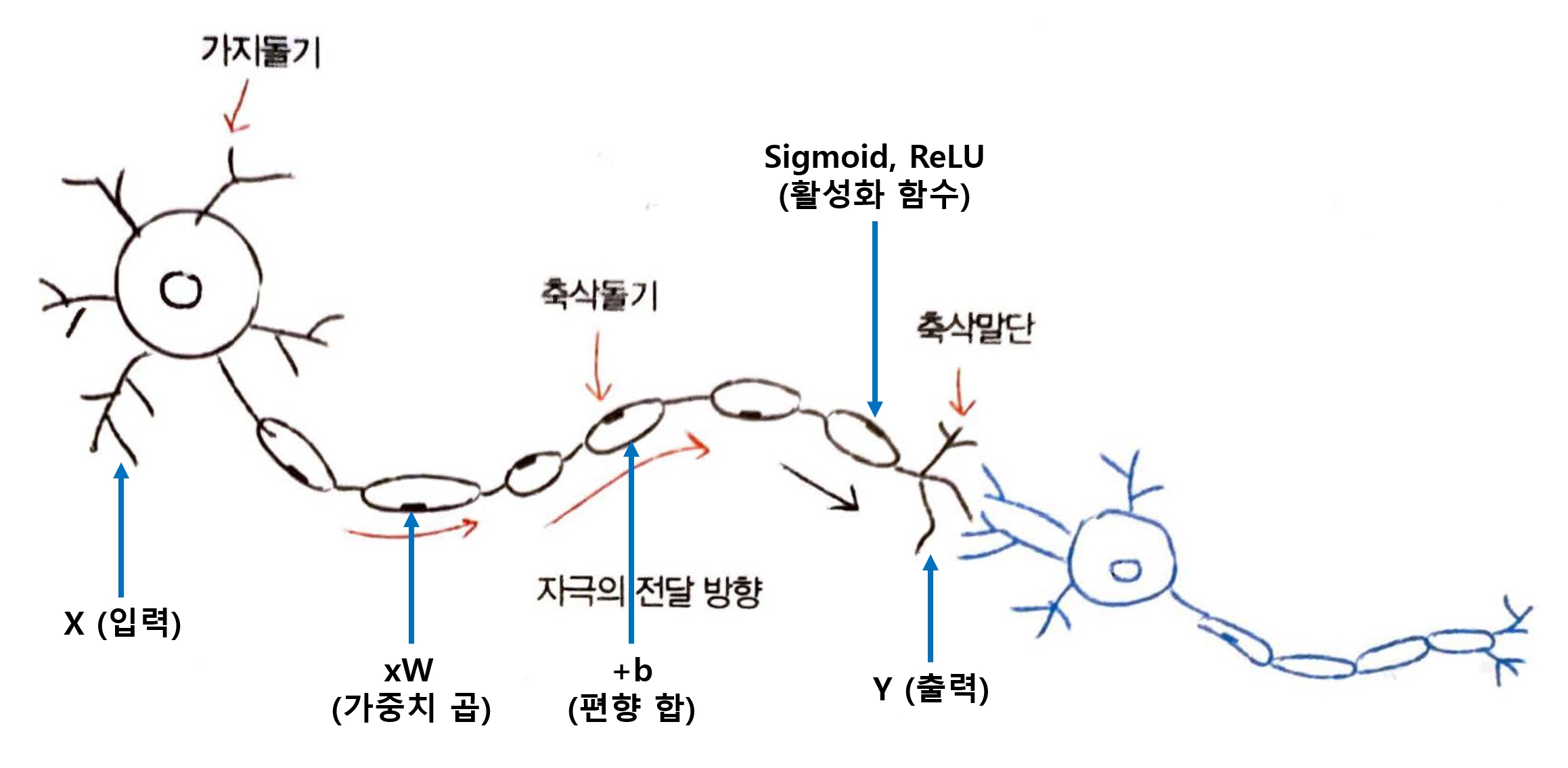
인공 뉴런의 기본 동작

• 입력 신호, 즉 입력값 X에 가중치(W) 를 곱하고 편향(b) 을 더함
• 그 다음 활성화 함수(Sigmoid, ReLU 등)를 거쳐 결과값 Y를 만들어 냄

학습(learning) or 훈련(training)

• 원하는 Y 값을 만들어내기 위해 W와 b의 값을 변경해가면서 적절한 값을 찾아내는 과정

활성화 함수 (activation function)

• 인공신경망을 통과해온 값을 최종적으로 어떤 값으로 만들지를 결정
• 인공 뉴런의 핵심 중에서도 가장 중요한 요소
• 대표적인 활성화 함수 : Sigmoid(시그모이드), ReLU(렐루), tanh(쌍곡탄젠트)

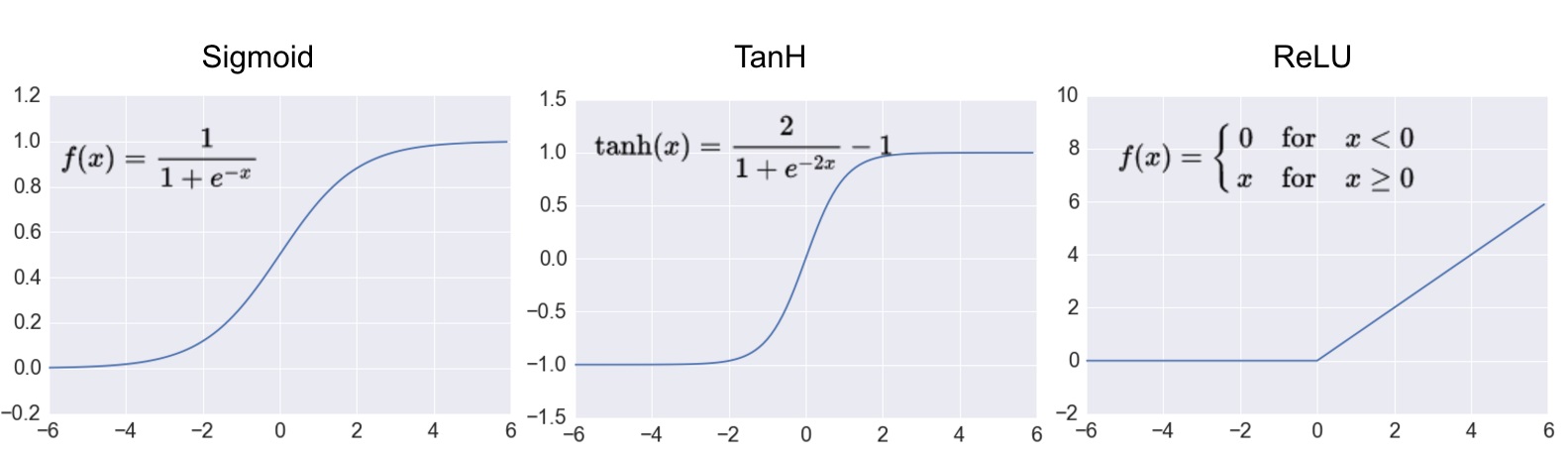
• 최근에는 활성화 함수로 ReLU 함수를 많이 사용
• ReLU 함수는 입력값이 0보다 작으면 항상 0을, 0보다 크면 입력값을 그대로 출력
• 학습 목적에 따라 다른 활성화 함수를 써야 하는 경우가 있음

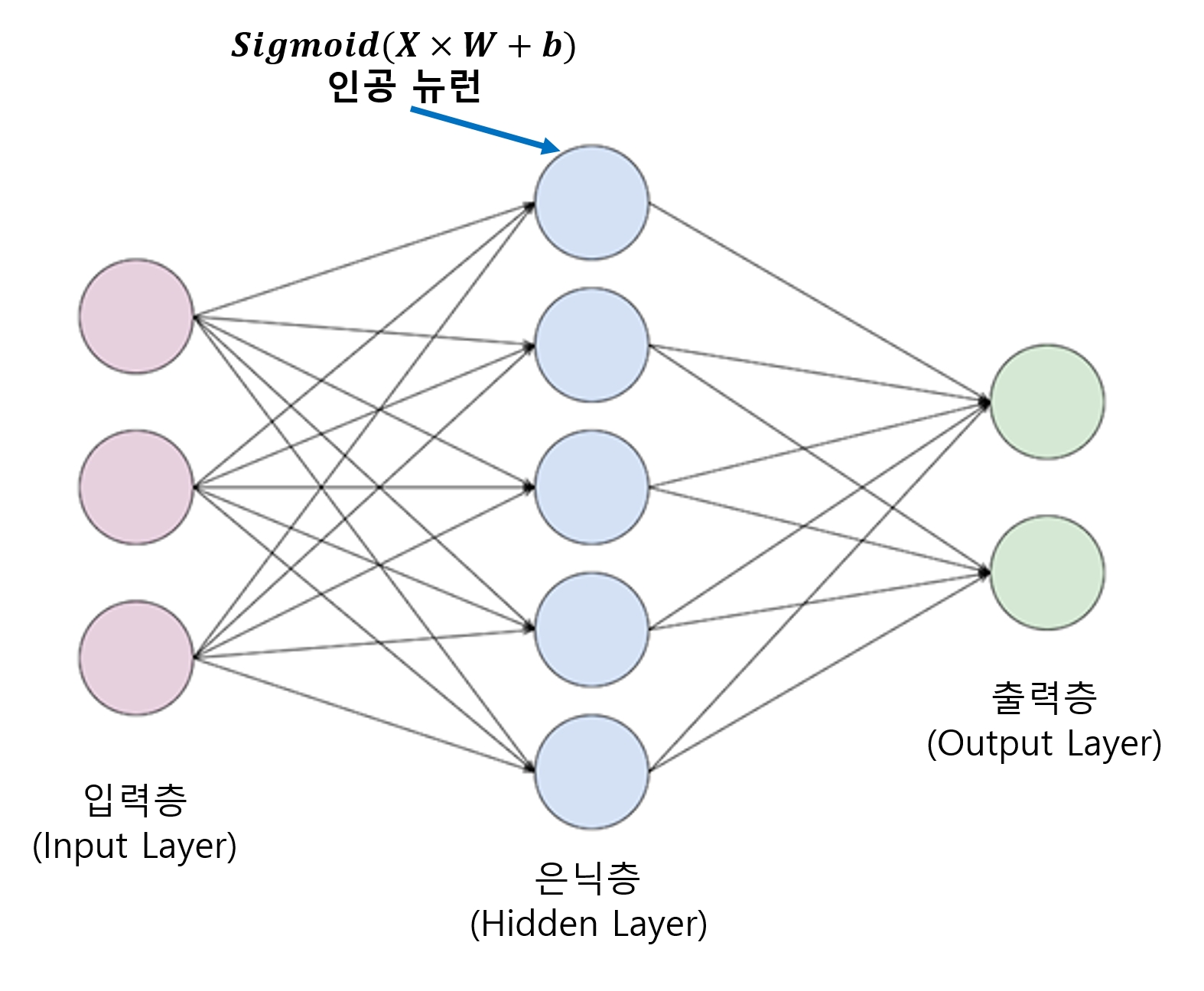
인공신경망

• 인공 뉴런을 충분히 많이 연결해놓는 것만으로 인간이 인지하기 어려운 매우 복잡한 패턴까지도 스스로 학습할 수 있게 된다.

4.1.2 딥러닝의 발전

• 수천 ~ 수만 개의 W와 b 값의 조합을 일일이 변경해가며 계산하려면 매우 오랜 시간이 걸리기 때문에 신경망을 제대로 훈련시키기 어려웠다.
• 신경망의 층이 깊어질수록 시도해봐야 하는 조합의 경우의 수가 기하급수적으로 늘어남
• 그렇기 때문에 과거에는 유의미한 신경망을 만들기란 거의 불가능하다고 여겨짐

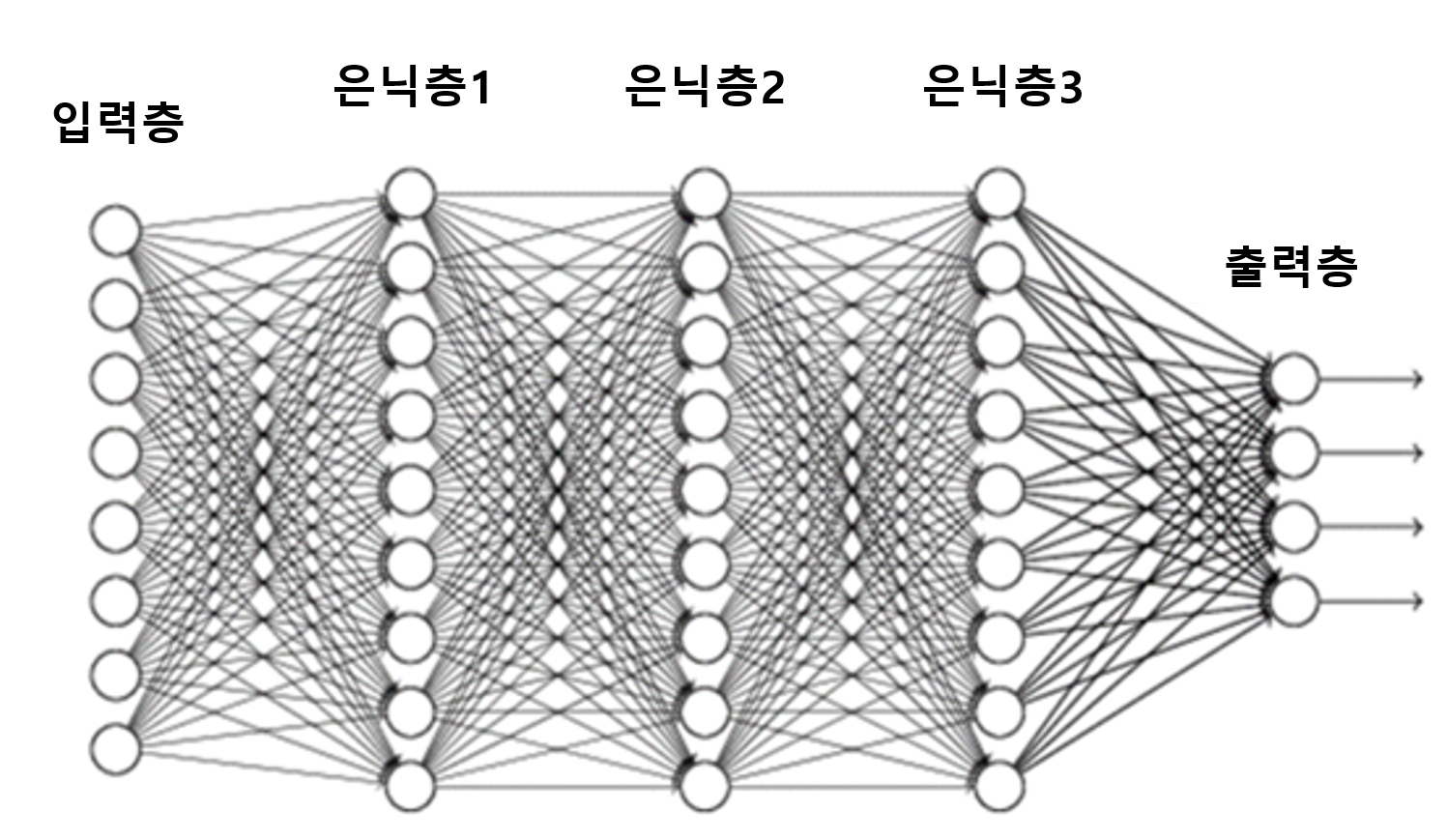
• 제프리 힌튼 (Geoffrey Hinton) 교수가 제한된 볼트만 머신(Restricted Boltzmann Machine, RBM) 이라는 신경망 학습 알고리즘을 개발
• 이 방법으로 심층 신경망을 효율적으로 학습시킬 수 있음을 증명
• 그 후 드롭아웃 기법, ReLU 등의 활성화 함수 들이 개발되면서 딥러닝 알고리즘은 급속한 발전을 이룸
• 데이터 양의 폭발적인 증가와 컴퓨팅 파워의 발전, 특히 단순한 수치 계산과 병렬 처리에 강한 GPU의 발전 또한 딥러닝 발전에 한 몫을 함

4.1.3 역전파(backpropagation)

• 역전파는 출력층이 내놓은 결과의 오차를 신경망을 따라 입력층까지 역으로 전파하며 계산해나가는 방식
• 이 방식은 입력층부터 가중치를 조절해가는 기존 방식보다 훨씬 유의미한 방식으로 가중치를 조절
• 최적화 과정이 훨씬 빠르고 정확해진다.

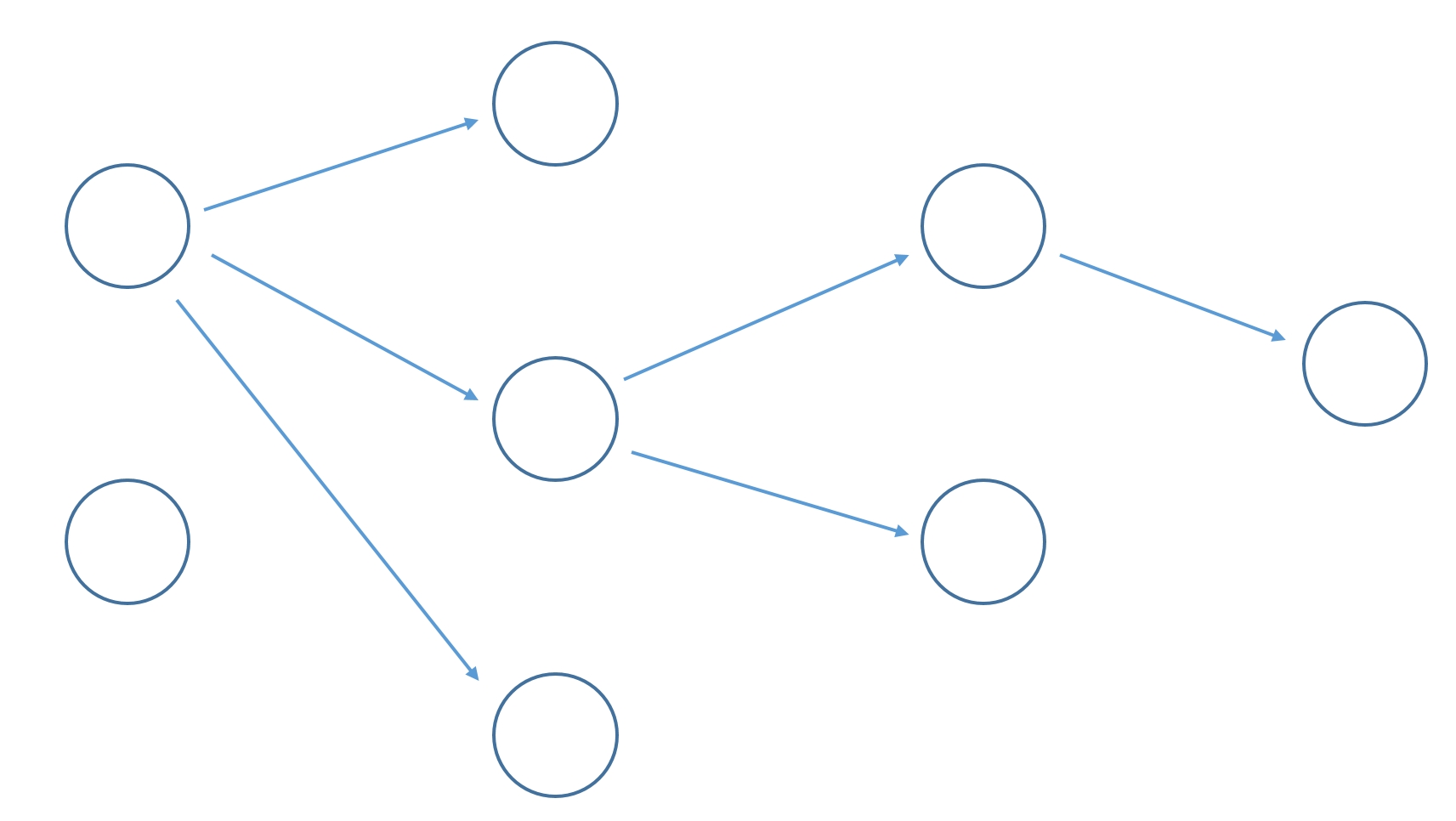
기본 학습 방법

• 모든 조합의 경우의 수에 대해 가중치를 대입하고 계산함

역전파

• 결과값의 오차를 앞쪽으로 전파하면서 가중치를 갱신함

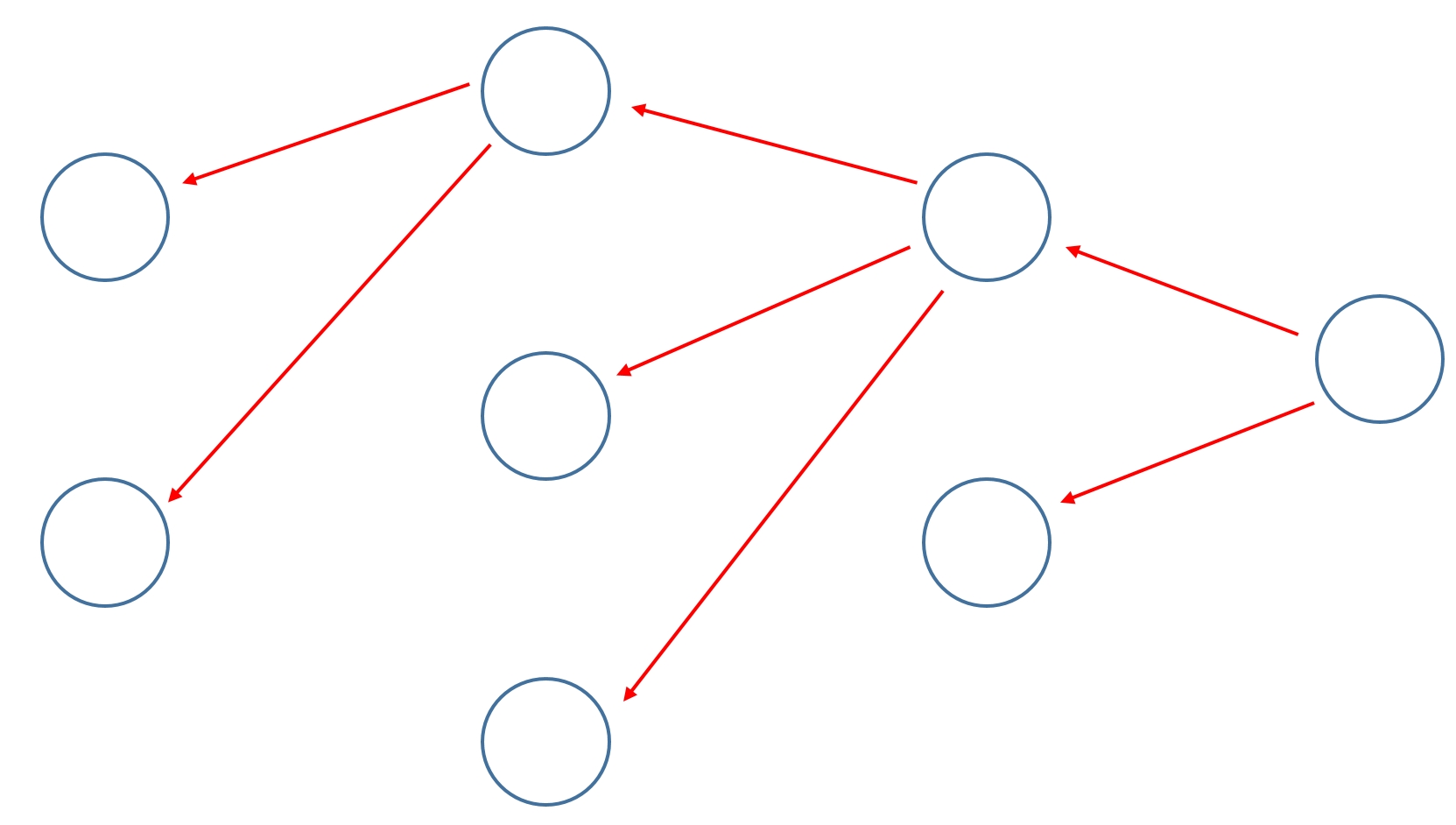
• 역전파는 신경망을 구현하려면 거의 항상 적용해야 하는 알고리즘이지만, 구현하기는 조금 어렵다.
• 텐서플로는 활성화 함수와 학습 함수 대부분에 역전파 기법을 기본으로 제공해줘서, 역전파를 따로 구현할 일은 거의 없다.
• 드롭아웃 알고리즘이나 ReLU 같은 활성화 함수도 직접 구현할 필요가 없다.
• 텐서플로를 사용하면 다양한 학습 알고리즘을 직접 구현하지 않고도 매우 쉽게 신경망을 만들고 학습할 수 있다.

4.2 간단한 분류 모델 구현하기

• 딥러닝이 가장 폭넓게 활용되는 분야 : 패턴 인식을 통한 영상 처리
• ex) 어떠한 사진이 고양이인지, 강아지인지 또는 자동차인지, 비행기인지 등을 판단하는 일

분류(classification)

• 위의 예와 같이 패턴을 파악해 여러 종류로 구분하는 작업

• 이번 예제에서는 털과 날개가 있느냐를 기준으로 포유류와 조류를 구분하는 신경망 모델 만들어봄
• 이미지 대신 간단한 이진 데이터 이용

4.2.1 라이브러리 임포트

• 텐서플로와 Numpy 라이프러리 임포트

Numpy 라이브러리

• 수치해석용 파이썬 라이브러리
• 행렬 조작과 연산에 필수
• 텐서플로도 Numpy를 매우 긴밀하게 이용

import tensorflow as tf
import numpy as np

4.2.2 데이터 정의

• 학습에 사용할 데이터 정의

1) 특징 데이터

• 털과 날개가 있느냐를 담은 특징 데이터를 구성
• 있으면 1, 없으면 0

# [털, 날개]
x_data = np.array([[0, 0], [1, 0], [1, 1], [0, 0], [0, 0], [0, 1]])

2) 레이블 데이터

• 각 개체가 실제 어떤 종류인지를 나타내는 레이블(분류값) 데이터 구성
• 앞서 정의한 특징 데이터의 각 개체가 포유류인지 조류인지, 아니면 제 3의 종류인지를 기록한 실제 결괏값
• 레이블 데이터는 원-핫 인코딩(one-hot encoding) 이라는 특수한 형태로 구성

원-핫 인코딩

• 데이터가 가질 수 있는 값들을 일렬로 나열한 배열을 만듬
• 그중 표현하려는 값을 뜻하는 인덱스의 원소만 1로 표기
• 나머지 원소는 모두 0으로 채우는 표기법

원-핫 인코딩 예제에 적용

• 우리가 판별하고자 하는 개체의 종류 3가지 : 기타, 포유류, 조류
• 이것들을 배열에 넣음 -> [기타, 포유류, 조류]
• 각 종류의 인덱스 : 기타=0, 포유류=1, 조류=2
• 이를 원-핫 인코딩 형식으로 만들면 다음과 같음

기타   = [1, 0, 0]
포유류 = [0, 1, 0]
조류   = [0, 0, 1]

• 각 종류에 해당하는 인덱스의 값만 1로 설정하고 나머지는 0으로 채움

• 특징 데이터와 연관 지어 레이블 데이터로 구성

y_data = np.array([[1, 0, 0], # 기타
                   [0, 1, 0], # 포유류
                   [0, 0, 1], # 조류
                   [1, 0, 0],
                   [1, 0, 0],
                   [0, 0, 1]])

• 이렇게 구성한 특징 데이터와 레이블 데이터는 다음과 같은 연관 관계를 갖게 된다.

# [털, 날개] -> [기타, 포유류, 조류]
[0, 0] -> [1, 0, 0] # 기타
[1, 0] -> [0, 1, 0] # 포유류
[1, 1] -> [0, 0, 1] # 조류
[0, 0] -> [1, 0, 0] # 기타
[0, 0] -> [1, 0, 0] # 기타
[0, 1] -> [0, 0, 1] # 조류

4.2.3 신경망 모델 구성

1) X, Y 플레이스홀더 설정

• 특징 X와 레이블 Y와의 관계를 알아내는 모델
• X와 Y에 실측값(ground truth) 을 넣어서 학습시킬 것이므로 X와 Y는 플레이스홀더로 설정

X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)

2) 가중치와 편향 변수 설정

• 신경망은 이 변수들의 값을 여러 가지로 바꿔가면서 X와 Y의 연관 관계를 학습하게 된다.

W = tf.Variable(tf.random_uniform([2, 3], -1., 1.))
b = tf.Variable(tf.zeros([3]))

• 가중치 변수 W : [입력층(특징 수), 출력층(레이블 수)]의 구성인 [2, 3]으로 설정
• 편향 변수 b : 레이블 수인 3개의 요소를 가진 변수로 설정

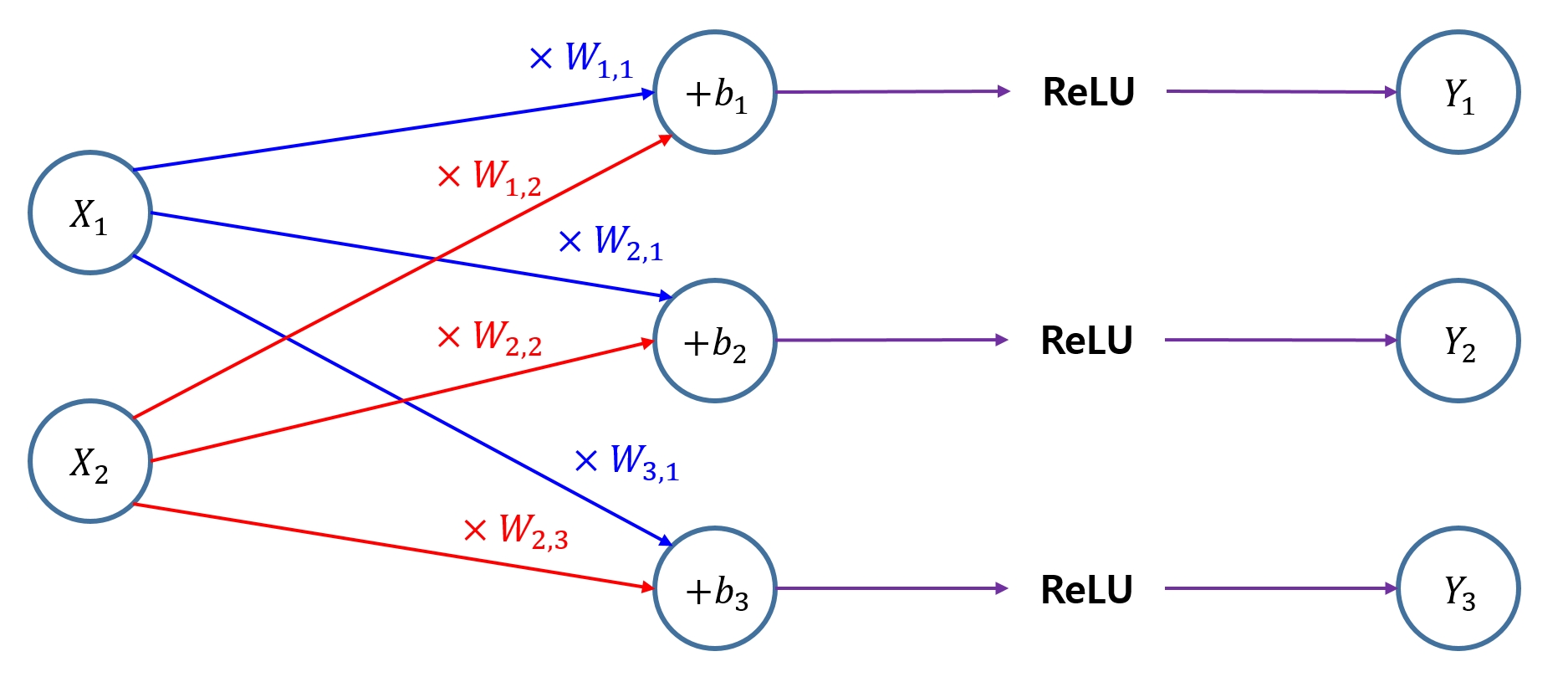
3) 활성화 함수 설정

• 이 가중치를 곱하고 편향을 더한 결과를 활성화 함수인 ReLU에 적용하면 신경망 구성은 끝난다.

L = tf.add(tf.matmul(X, W), b)
L = tf.nn.relu(L)

• 이렇게 구성한 신경망은 아래 그림과 같이 나타낼 수 있다.

4.2.4 softmax 함수

• 신경망을 통해 나온 출력값을 softmax 함수 를 이용하여 사용하기 쉽게 다듬어준다.

model = tf.nn.softmax(L)

softmax 함수

• 다음처럼 배열 내의 결과값들을 전체 합이 1이 되도록 만들어 줌
• 전체가 1이니 각각은 해당 결과의 확률로 해석할 수 있다.

[8.04, 2.76, -6.52] -> [0.53, 0.24, 0.23]

4.2.5 손실 함수

• 손실 함수는 원-핫 인코딩을 이용한 대부분의 모델에서 사용하는 교차 엔트로피(Cross-Entropy) 함수를 사용

1) 교차 엔트로피(Cross-Entropy)

• 교차 엔트로피 값은 예측값과 실제값 사이의 확률 분포 차이를 계산한 값
• 기본 코드는 다음과 같다.

cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(model), axis=1))

\[cost = \frac {1} {m}\sum _{t =1}^{m}\left( -\sum \left\{ Y\times \log \left( \overline {Y} \right) \right\} \right)\]

NOTE

• 손실 함수는 비용 함수(cost function) 라고도 한다.

2) 계산 과정 확인

(1) Y 와 model

• Y : 실측값
• model : 신경망을 통해 나온 예측값

    Y           model
[[1 0 0]   [[0.1 0.7 0.2]
 [0 1 0]]   [0.2 0.8 0.0]]

(2) model 값에 log를 취한 값을 Y와 곱하기

    Y           model          Y * tf.log(model)
[[1 0 0]   [[0.1 0.7 0.2]   -> [[-1.0     0 0]
 [0 1 0]]   [0.2 0.8 0.0]]      [   0 -0.09 0]]

(3) 행별로 값을 다 더함

Y * tf.log(model)     reduce_sum(axis=1)
[[-1.0     0 0]    -> [-1.0, -0.09]
 [   0 -0.09 0]]

(4) 배열 안의 값의 평균 계산

reduce_sum         reduce_mean
[-1.0, -0.09]  ->  -0.545

• 이 값이 우리의 손실값인 교차 엔트로피 값이 된다.

NOTE

• reduce_xxx 함수들은 텐서의 차원을 줄여준다.
• 함수 이름의 xxx 부분이 구체적인 차원 축소 방법을 뜻함
• axis 매개변수로 축소할 차원을 정함
• ex1) reduce_sum(<입력텐서>, axis=1) : 주어진 테서의 1번째 차원의 값들을 다 더해(값 1개로 만들어서) 그 차원을 없앤다는 뜻
• sum 외에 prod, min, max, mean, all(논리적 AND), any(논리적 OR), logsumexp 등을 제공
• 자세한 설명은 문서 를 참고

4.2.6 학습

• 텐서플로가 기본 제공하는 최적화 함수 사용

# 기본적인 경사하강법으로 최적화
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train_op = optimizer.minimize(cost)

# 텐서플로의 세션을 초기화
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

# 앞서 구성한 특징과 레이블 데이터를 이용해 학습을 100번 진행
for step in range(100):
    sess.run(train_op, feed_dict={X: x_data, Y: y_data})

    # 학습 도중 10번에 한 번씩 손실값을 출력
    if (step + 1) % 10 == 0:
        print(step+1, sess.run(cost, feed_dict={X: x_data, Y: y_data}))

10 1.1570371
20 1.1457922
30 1.1365778
40 1.1276896
50 1.1190915
60 1.1108141
70 1.1027659
80 1.0950179
90 1.0875193
100 1.0803043

4.2.7 학습 결과 확인

• 학습된 결과를 확인해보는 코드 작성

prediction = tf.argmax(model, axis=1)
target = tf.argmax(Y, axis=1)
print('예측값: ', sess.run(prediction, feed_dict={X: x_data}))
print('실제값: ', sess.run(target, feed_dict={Y: y_data}))

예측값:  [2 0 2 2 2 1]
실제값:  [0 1 2 0 0 2]

1) argmax 함수

• 예측값인 model을 바로 출력하면 [0.2 0.7 0.1]과 같이 확률로 나옴
• 그렇기 때문에 요소 중 가장 큰 값의 인덱스를 찾아주는 argmax 함수를 사용하여 레이블 값을 출력
• 즉, 다음처럼 원-핫 인코딩을 거꾸로 한 결과를 만들어 준다.

[[0 1 0] [1 0 0]] -> [1 0]
[[0.2 0.7 0.1] [0.9 0.1 0.]] -> [1 0]

4.2.8 정확도 출력

is_correct = tf.equal(prediction, target)
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
print('정확도: %.2f' % sess.run(accuracy * 100, feed_dict={X: x_data, Y: y_data}))

정확도: 16.67

1) tf.equal

• 전체 학습 데이터에 대한 예측값과 실측값을 tf.equal 함수로 비교
• 비교 결과는 true/false 값으로 나옴

2) tf.cast

• tf.equal 함수 결과를 다시 tf.cast 함수를 이용해 0과 1로 바꾸어 평균을 내면 간단히 정확도를 구할 수 있다.

• 손실값이 점점 줄어드는 것 확인 가능
• 하지만 학습 횟수를 아무리 늘려도 정확도가 크게 높아지지 않는다.
• 그 이유는 신경망이 한 층밖에 안되기 때문
• 층 하나만 더 늘리면 쉽게 해결 된다.

4.2.9 전체 코드

# 4.2.1
import tensorflow as tf
import numpy as np

# 4.2.2
x_data = np.array([[0, 0], [1, 0], [1, 1], [0, 0], [0, 0], [0, 1]])
y_data = np.array([[1, 0, 0], # 기타
                   [0, 1, 0], # 포유류
                   [0, 0, 1], # 조류
                   [1, 0, 0],
                   [1, 0, 0],
                   [0, 0, 1]])

# 4.2.3
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)

W = tf.Variable(tf.random_uniform([2, 3], -1., 1.))
b = tf.Variable(tf.zeros([3]))

L = tf.add(tf.matmul(X, W), b)
L = tf.nn.relu(L)

# 4.2.4
model = tf.nn.softmax(L)

# 4.2.5
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(model), axis=1))

# 4.2.6
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train_op = optimizer.minimize(cost)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

for step in range(100):
    sess.run(train_op, feed_dict={X: x_data, Y: y_data})

    # 학습 도중 10번에 한 번씩 손실값을 출력
    if (step + 1) % 10 == 0:
        print(step+1, sess.run(cost, feed_dict={X: x_data, Y: y_data}))

# 4.2.7
prediction = tf.argmax(model, axis=1)
target = tf.argmax(Y, axis=1)
print('예측값: ', sess.run(prediction, feed_dict={X: x_data}))
print('실제값: ', sess.run(target, feed_dict={Y: y_data}))

# 4.2.8
is_correct = tf.equal(prediction, target)
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
print('정확도: %.2f' % sess.run(accuracy * 100, feed_dict={X: x_data, Y: y_data}))

10 1.153698
20 1.1510115
30 1.1483516
40 1.1457175
50 1.1431087
60 1.1405246
70 1.1379647
80 1.1354283
90 1.132915
100 1.1304244
예측값:  [0 1 1 0 0 1]
실제값:  [0 1 2 0 0 2]
정확도: 66.67

4.3 심층 신경망 구현하기

• 신경망의 층을 둘 이상으로 구성한 심층 신경망, 즉, 딥러닝을 구현

4.3.1 가중치와 편향 추가

• 앞서 만든 신경망 모델에 가중치와 편향을 추가

W1 = tf.Variable(tf.random_uniform([2, 10], -1., 1.))
W2 = tf.Variable(tf.random_uniform([10, 3], -1., 1.))

b1 = tf.Variable(tf.zeros([10]))
b2 = tf.Variable(tf.zeros([3]))

• 첫 번째 가중치의 형태 : [2, 10]
• 두 번째 가중치의 형태 : [10, 3]
• 편향은 각각 10과 3으로 설정
• 그 의미는 다음과 같음

# 가중치
W1 = [2, 10] -> [특징, 은닉층의 뉴런 수]
W2 = [10, 3] -> [은닉층의 뉴런 수, 분류 수]

# 편향
b1 = [10] -> 은닉층의 뉴런 수
b2 = [3]  -> 분류 수

• 입력층과 출력층은 각각 특징과 분류 개수로 맞춤
• 중간 연결 부분은 맞닿은 층의 뉴런 수와 같도록 맞추면 된다.

은닉층(hidden layer)

• 중간의 연결 부분
• 은닉층의 뉴런 수는 하이퍼파라미터 이므로 실험을 통해 가장 적절한 수를 정하면 된다.

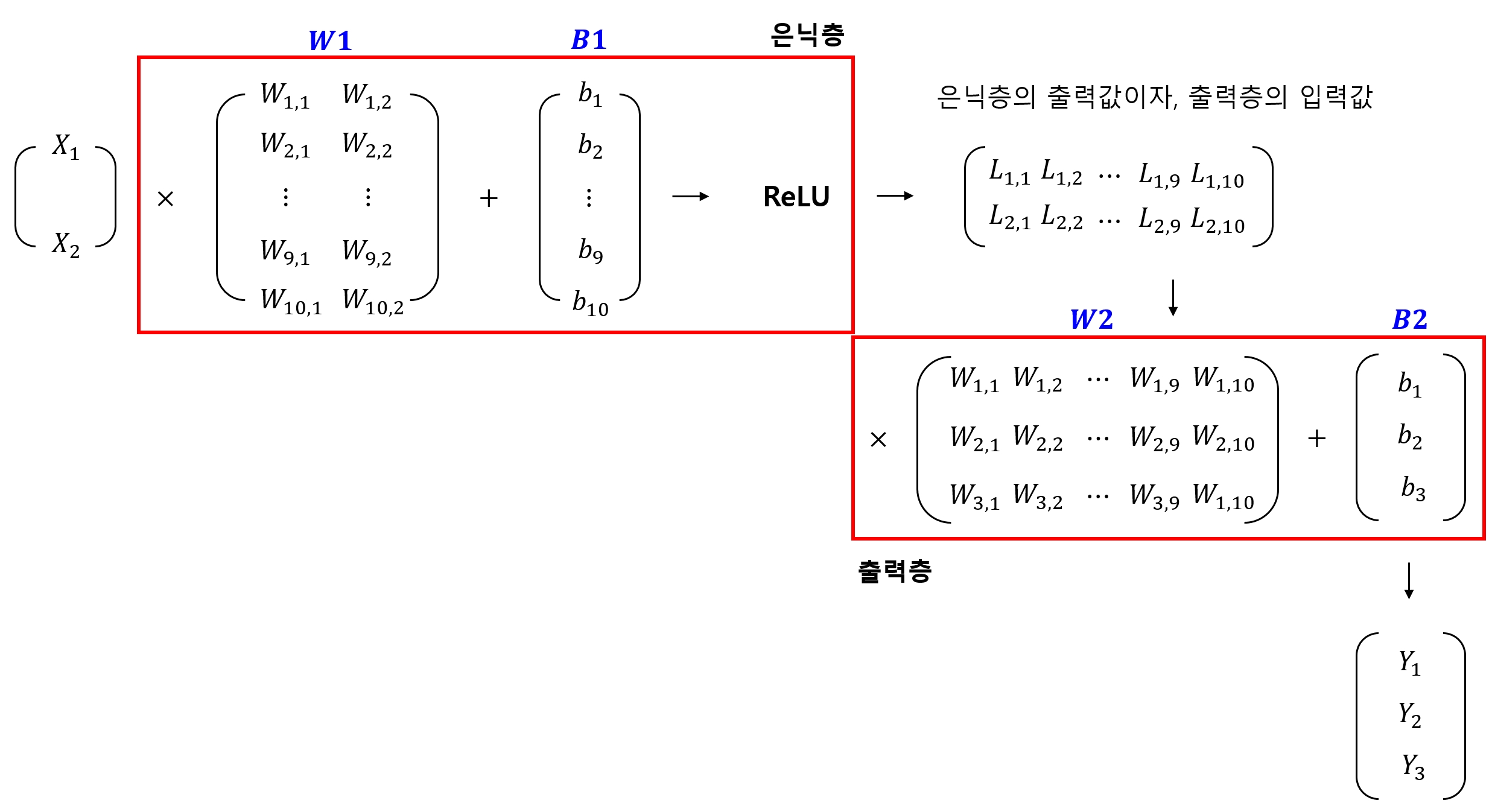
4.3.2 활성화 함수 적용

• 특징 입력값에 첫 번째 가중치와 편향, 그리고 활성화 함수 적용

L1 = tf.add(tf.matmul(X, W1), b1)
L1 = tf.nn.relu(L1)

4.3.3 최종 모델 생성

• 두 번째 가중치와 편향을 적용하여 최종 모델을 만듬
• 은닉층에서 두 번째 가중치 W2[10, 3]와 편향 b2[3]을 적용하면 최종적으로 3개의 출력값을 가지게 됨

model = tf.add(tf.matmul(L1, W2), b2)

NOTE

• 기본 신경망 모델에서는 출력층에 활성화 함수 적용했지만, 사실 출력층에는 활성화 함수를 사용하지 않는다.
• 하이퍼파라미터와 마찬가지로 은닉층과 출력층에서 활성화 함수를 적용할 지 말지, 또 어떤 활성화 함수를 적용할지 정하는 일 또한 신경망 모델을 만드는 경험적, 실험적 요소이다.

4.3.4 손실함수 작성

• 손실 함수로 교차 엔트로피 함수 사용
• 이번엔 텐서플로가 기본 제공하는 교차 엔트로피 함수 이용

cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=Y, logits=model))
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train_op = optimizer.minimize(cost)

• 최적화 함수로 AdamOptimizer 사용
• AdamOptimizer가 GradientDescentOptimizer 보다 성능이 좋다고 알려짐
• 하지만 모든 경우에 좋은 것은 아님
• 이 링크 에서 다양한 최적화 함수 참고

4.3.5 학습 진행, 손실값과 정확도 측정

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

# 학습 진행
for step in range(100):
    sess.run(train_op, feed_dict={X: x_data, Y: y_data})

    # 손실값 측정
    if (step + 1) % 10 == 0:
        print(step+1, sess.run(cost, feed_dict={X: x_data, Y: y_data}))

# 학습결과 확인
prediction = tf.argmax(model, axis=1)
target = tf.argmax(Y, axis=1)

print("예측값: ", sess.run(prediction, feed_dict={X: x_data}))
print("실제값: ", sess.run(target, feed_dict={Y: y_data}))

# 정확도 측정
is_correct = tf.equal(prediction, target)
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
print('정확도: %.2f' % sess.run(accuracy * 100, feed_dict={X: x_data, Y: y_data}))

10 1.1107937
20 0.901318
30 0.7599769
40 0.6542157
50 0.5529445
60 0.46028176
70 0.37929973
80 0.31116098
90 0.2555883
100 0.20859426
예측값:  [0 1 2 0 0 2]
실제값:  [0 1 2 0 0 2]
정확도: 100.00

4.3.6 전체 코드

import tensorflow as tf
import numpy as np

x_data = np.array([[0, 0], [1, 0], [1, 1], [0, 0], [0, 0], [0, 1]])
y_data = np.array([[1, 0, 0],
                   [0, 1, 0],
                   [0, 0, 1],
                   [1, 0, 0],
                   [1, 0, 0],
                   [0, 0, 1]])

X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)

# 4.3.1
W1 = tf.Variable(tf.random_uniform([2, 10], -1., 1.))
W2 = tf.Variable(tf.random_uniform([10, 3], -1., 1.))

b1 = tf.Variable(tf.zeros([10]))
b2 = tf.Variable(tf.zeros([3]))

# 4.3.2
L1 = tf.add(tf.matmul(X, W1), b1)
L1 = tf.nn.relu(L1)

# 4.3.3
model = tf.add(tf.matmul(L1, W2), b2)

# 4.3.4
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels=Y, logits=model))

optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train_op = optimizer.minimize(cost)

# 4.3.5
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

for step in range(100):
    sess.run(train_op, feed_dict={X: x_data, Y: y_data})

    if (step + 1) % 10 == 0:
        print(step+1, sess.run(cost, feed_dict={X: x_data, Y: y_data}))

prediction = tf.argmax(model, axis=1)
target = tf.argmax(Y, axis=1)

print("예측값: ", sess.run(prediction, feed_dict={X: x_data}))
print("실제값: ", sess.run(target, feed_dict={Y: y_data}))

is_correct = tf.equal(prediction, target)
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
print('정확도: %.2f' % sess.run(accuracy * 100, feed_dict={X: x_data, Y: y_data}))

10 1.2039233
20 0.9245847
30 0.7352774
40 0.6101547
50 0.5018402
60 0.40505704
70 0.31671748
80 0.236906
90 0.17302088
100 0.12656452
예측값:  [0 1 2 0 0 2]
실제값:  [0 1 2 0 0 2]
정확도: 100.00