Monte Carlo

ML study > Reinforcement Learning > Monte Carlo

1. Sampling

• 지금까지 State transition probability와 같은 MDP의 환경이 주어졌을 때 bellman equation 을 푸는 Dynamic programming에 대해 알아보았다. 이 방식의 문제는 환경을 모를때 적용할 수 없고 모든 table에 대해 update 하기 때문에 계산이 매우 많다는 점이 있었다.

• 이러한 문제를 해결하기 위해 모든 table에 대해 update하는 full width back up 이 아닌 일부분을 sampling 하여 update 하는 sample backup 방식을 적용할 수 있다.

Source

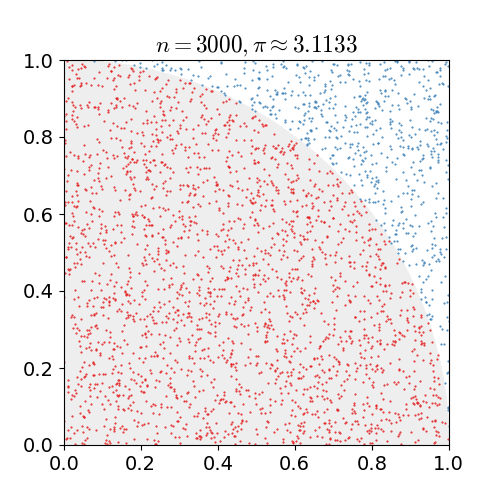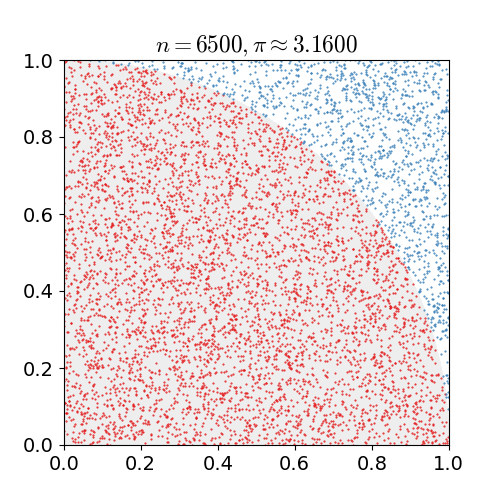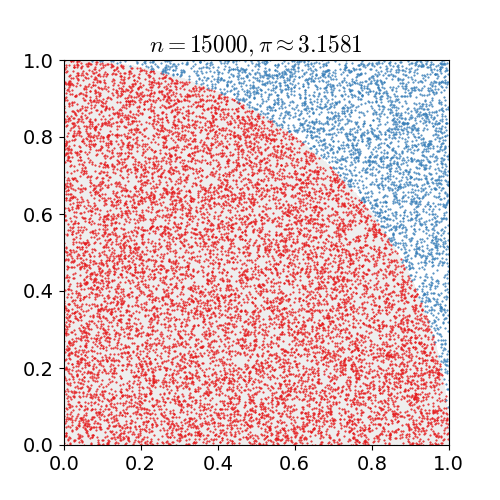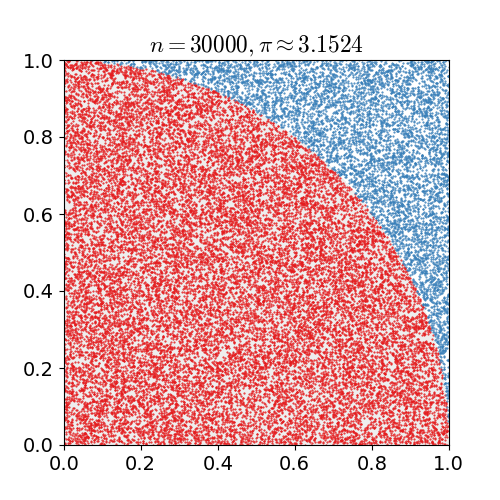
• 예를 들어 원주율을 계산하기 위해 위 그림과 같이 πR²/4 = 원의 넓이/4 같은 수식을 세웠다고 하자. 수식으로 부터 원의 넓이만 알고 있다면 우리는 원주율 π를 구할 수 있다. 하지만 원의 넓이를 모른다고 가정했을 때 우리는 사각형 안에 점을 임의로 수많이 뿌려서 총 점의 개수와 원안에 들어온 점의 개수의 비율을 구함으로써 우리는 원의 넓이를 예측해낼 수 있다. 즉, πR²/4 = 원의 넓이/4 = 빨간점의 수/ 점의 수 라는 수식을 세워 원주율을 계산할 수 있게 된다. 점의 개수를 무수히 많이 뿌린다면 결국 실제 원과 사각형의 비율대로 점의 개수가 나타날 것이기 때문이다.

• 이러한 방식을 sampling 이라고 하며 그 중 대표적인 방식인 Monte Carlo 방식에 대해 알아볼 것이다.

2. Monte Carlo

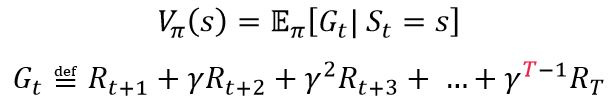
• 모델의 환경을 아는 경우 value function 값은 직접 state transition probability를 고려하여 expectation 값을 계산했지만 Monte Carlo 방식의 경우 위 수식에서 보듯이 Value function은 해당 정책 π를 따라 episode가 끝났을 때 실제로 받은 return 값으로 나타난다. 이 때 G_t를 여러번 시뮬레이션해서 평균을 계산해주면 실제 Vπ(s)와 값이 비슷해질 것이다. 이러한 방식의 sampling 과정을 Monte Carlo라고 부른다. 행동 가치함수 역시 동일한 과정을 통해 계산할 수 있다.

2.1 First-visit Monte Carlo policy evaluation

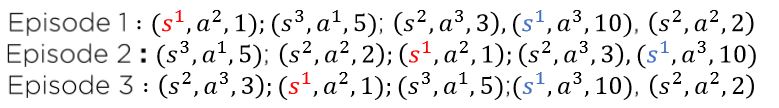
• Monte Carlo의 경우 정책 π를 따라 episode가 끝날 때까지 진행하게 되는데 문제는 위와 같이 같은 state를 여러번 지나게 되는 경우가 발생할 수 있다. 이러한 경우 최초로 방문한 s1에 대해서만 return을 계산하는 방식이 first-visit MC policy evaluation이다.

2.1 Every-visit Monte Carlo policy evaluation

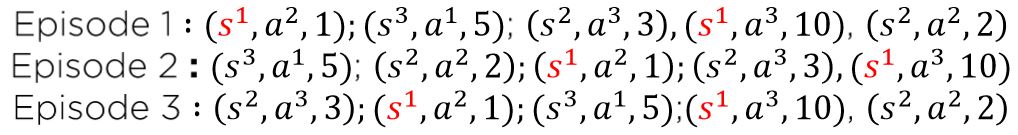
• 한편 위와 같이 지나온 state (s1) 에 대해서 모두 return을 계산하게 되는 경우 Every-visit MC policy evaluation 이라고 부른다.

2.3 Incremental Monte Carlo policy evaluation

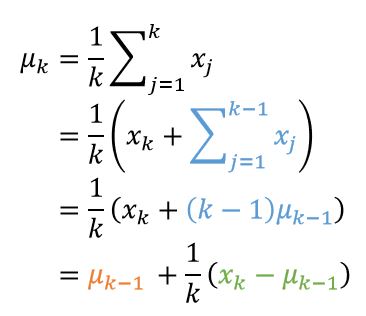
• MC의 return을 계산할 때 모든 episode에 대한 return값을 저장한 뒤 평균을 내면 메모리소모가 커지게 된다. 이 때, 위 수식 처럼 평균을 구하는 방법을 풀어서 나타내면 결국 이전의 평균값과 현재의 데이터만을 가지고 새로운 평균 값을 구할 수 있다. 이러한 방식을 Incremental Monte Carlo policy evaluation 이라고 한다.

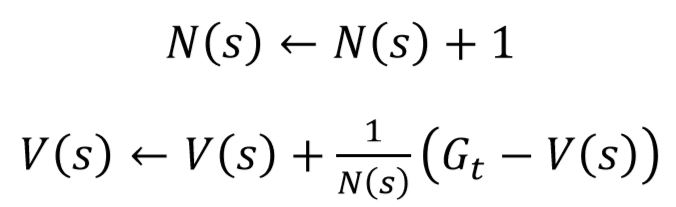
• 즉 value function의 update 관점에서 위 수식과 같이 표현가능하다.

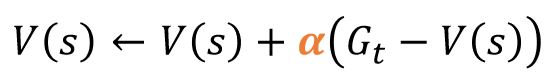
• 이 때,현실에선 이 N(s)값을 구하는 것조차 어려워 질 수 있기 때문에 일반적으로 적당히 작은 알파값을 임의로 주어 계산을 한다.

Reference

[1]: Reinforcement learning: an introduction

[2]: Fundamental of Reinforcement Learning

[3]: Fast Campus 강의자료

[4]: Silver 교수님 강의자료