Bellman Equation

ML study > Reinforcement Learning > Bellman Equation

1. MDP의 목표

• 강화학습의 문제는 MDP로 정의가 가능하다. 그렇다면 MDP의 최종 목표는 무엇일까? MDP의 구성요소인 Reward를 최대로 받는 것이다. 최대의 보상을 받도록 행동을 결정한다면 그것이 최적의 행동이 될 것이다.

1.1 Return

• 특정 state에서만 높은 reward를 받는다고 해서 MDP의 목표를 이루었다고 할 수는 없다. 따라서 특정 state 부터 마지막 state까지 받은 reward의 합을 계산하는 것이 매우 중요하며 이 값을 우리는 return이라고 부른다.

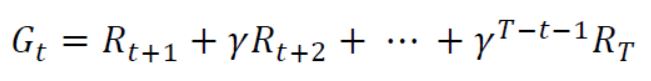
• Return은 위 수식과 같이 표현할 수 있다. R은 각 state에서의 보상이며 γ는 감가율을 의미한다.

2. Bellman Expectation Equation

2.1 Value function

• Return은 결국 episode가 끝난 뒤에 계산할 수 있다. 하지만 우리는 어떠한 state (s) 에서 받을 것이라 예상되는 return의 기댓값을 다음과 같이 정의할 수 있으며 이를 value function (가치함수) 라고 부른다.

2.2 Bellman Expectation Equation for value function

• 앞서 정의한 가치함수를 기존 return의 정의에 따라 풀어써주고 정리하면 state (s) 에서의 가치함수는 다음 state에서 받은 reward와 감마율을 곱한 다음 state (s_t+1) 의 가치함수에 대한 기댓값으로 표현가능하다.

• 이렇게 정의된 식을 우리는 Bellman expectation equation이라고 부른다.

2.3 Action value function

• Return에 대한 기댓값을 특정 state에서도 계산을 할 수 있지만 state에서 action까지 했을 경우 받을 수 있는 return에 대해서도 다음 수식과 같이 정의할 수 있다.

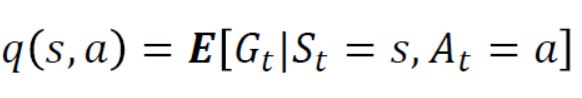
2.4 Bellman Expectation Equation for action value function

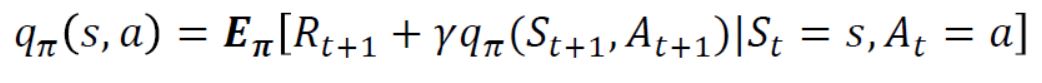
• 가치함수에서 bellman expectation equation을 유도했던 방식과 동일하게 유도하면 위와 같은 큐함수에 대한 bellman expectation equation을 정의할 수 있게 된다.

2.5 Relation between value function and action value function

• 가치함수는 state(s) 에서 받을 것이라 예측되는 return의 기댓값이었고 행동가치함수는 s에서 action(a)를 했을 때 받을 수 있는 return의 기댓값으로 정의되었다.

• 따라서 가치함수는 다음 수식과 같이 s에서 계산될 수 있는 q 함수에 대한 기댓값으로 나타낼 수 있다.

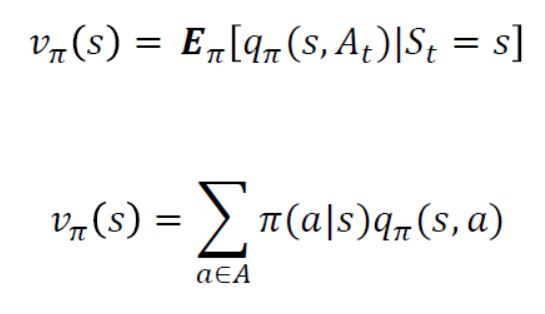
3. Bellman Optimality Equation

• 지금까지 가치함수와 행동가치함수에 대한 bellman expectation equation을 유도해보았다. 이 수식으로 부터 우리는 각각의 가치함수를 계산할 수 있게 되는데 이것이 강화학습의 최종목적이 아니었다.

• MDP의 목표는 앞서 살펴보았듯이 가장 높은 return을 얻을 수 있는 최적의 정책 𝜋를 찾는 것이다. 마찬가지로 최적의 정책 𝜋를 따라 가치함수와 행동가치함수를 계산하면 최적의 함수를 찾을 수 있을 것이다.

• 이 때의 함수를 Bellman optimality equation이라고 말하며 다음과 같이 표현이 가능하다.

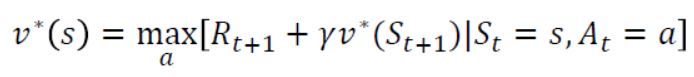
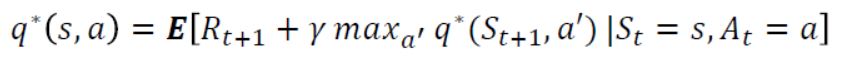
• 가치 함수의 경우 최적의 정책 𝜋를 따라 계산하게 되면 s에서 최적의 행동가치함수를 계산해주면 되므로 기댓값없이 표현이 가능하다. 행동 가치함수의 경우 s에서 a를 했을 때 state transition probability를 고려해주어야 하기 때문에 다음 행동가치함수가 max가 되게 하는 값의 expectation 값으로 나타낼 수 있는 것이다.

• 이로써 우리는 MDP의 목표를 이루기 위한 equation 유도를 마쳤다. 하지만 이 함수들은 linear한 함수가 아니기 때문에 주어진 값으로 부터 해를 바로 구할 수 없다. 다음 post에서는 bellman optimality equation을 푸는 방법에 대해 알아볼 것이다.

Reference

[1]: Reinforcement learning: an introduction

[2]: Fundamental of Reinforcement Learning

[3]: Fast Campus 강의자료