ML study > Reinforcement Learning > Monte Carlo Control
1. Generalized Policy Iteration
-
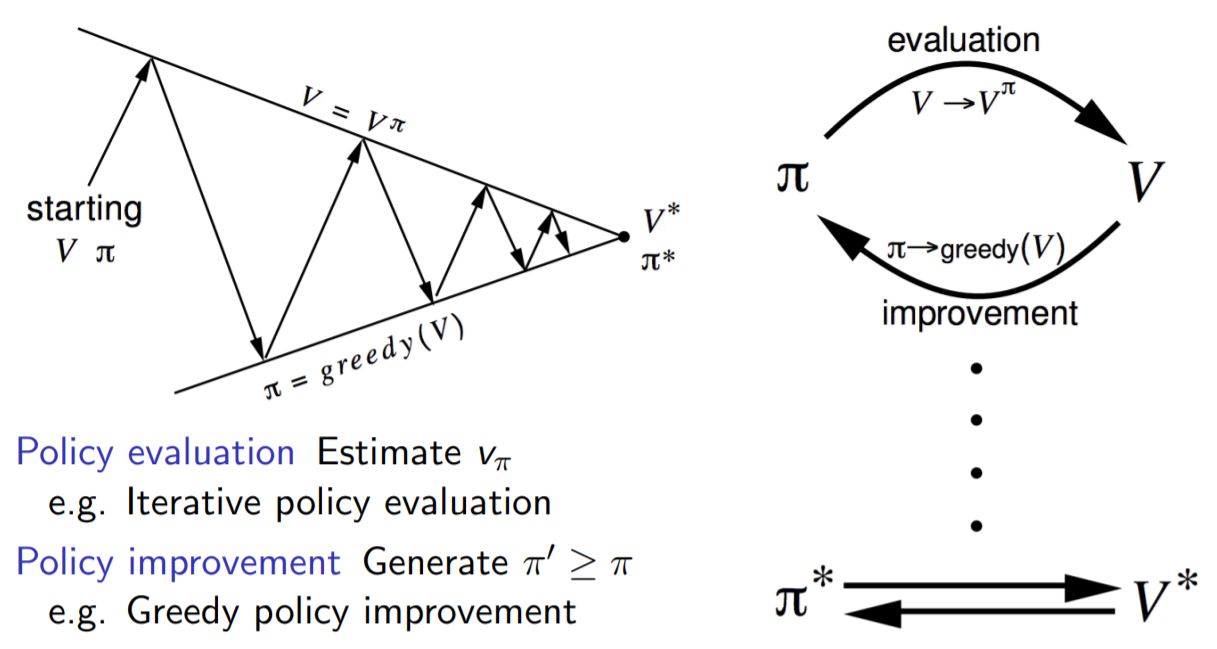
앞선 Dynamic programming 에서 우리는 bellman expectation equation을 policy iteration 과정을 통해 풀었었다.
-
하나의 Iteration은 어떤 policy에 대하여 value function을 구하는 prediction 과정과 더 나은 policy를 구하는 control 과정을 포함한다. 이때 prediction문제는 evaluation을 통해, control 문제는 improvement를 통해 풀게 된다. 가끔 헷갈릴 수 있는 용어이므로 잘 정리해둘 필요가 있다.
-
DP에서와 마찬가지로 MC에서 우리는 evaluation 하는 과정을 앞선 post에서 알아보았다. 이번 post에서는 MC에서 control 문제를 해결하는 방법에 대해 알아볼 것이다.
2. MC Control

-
MC 에서도 DP와 마찬가지로 policy를 control을 greedy한 value function을 가지는 policy로 improve 한다고 가정하면 새로운 policy는 위와 같이 구해질 것이다. 이 때 value function을 가지고 새로운 policy를 구하게 되면 model의 환경을 알아야하기 때문에 MC의 control 문제는 evaluation과정을 통해 구한 행동가치함수를 사용하게 된다.
-
하지만 모든 table에 대해 계산하며 iteration을 거쳤던 DP와는 달리 MC는 일부분에 대해서 update가 되기 때문에 policy 를 improve 할 때 무조건 greedy한 policy를 선택하게 된다면 문제가 될 수도 있다. 실제로 다른 행동을 했을 때 더 좋은 return 값을 가질 수 있기 때문이다.

-
따라서 MC control에서 정책 π는 행동가치함수에 대하여 무조건 greedy한 action을 취하는 것이 아니라 ε의 확률로는 모든 가능한 행동 중 하나를 임의로 선택하도록 하는 ε-greedy 방식을 통해 policy control 문제를 해결할 수 있다.
-
직관적으로 ε-greedy 방식이 정책개선을 이루어낼 수 있다는 것을 보았지만 수식적으로도 확인이 가능하다.
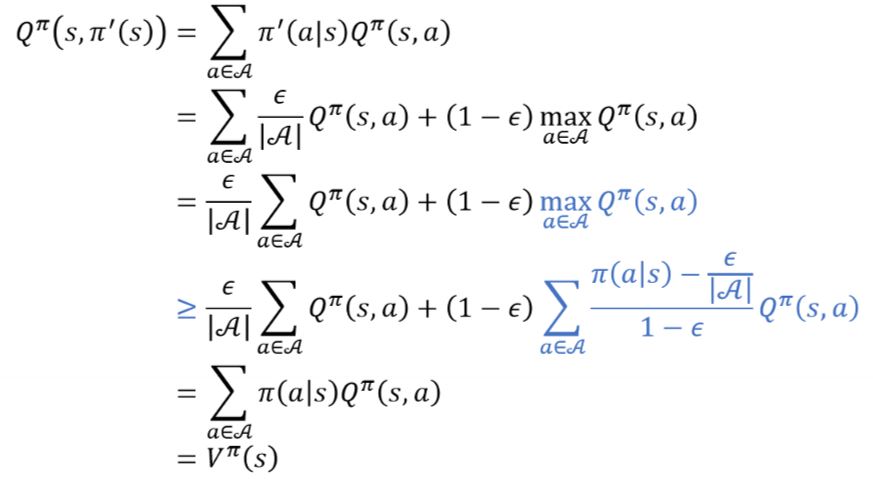
-
개선된 정책으로 부터 나오는 Q함수를 풀어서 적으면 위와 같이 차례로 유도가 가능하다.
-
이 때 3번째에서 4번째줄로 넘어갈 때, 파란색으로 칠한 부분이 한번에 이해가 어려울 수 있다. 4번째 나오는 시그마 term을 합하면 결국 1이 된다는 것은 알 수 있는데 이 값이 Q함수와 곱해져서 더한 값은 결국 Q함수의 max 값보다는 같거나 작을 수 밖에 없다. 따라서 3번째에서 4번째 줄로 넘어가게 되며 이후는 계산 및 정의를 통해 넘어갈 수 있다.
-
즉, Vπ’ 값은 Vπ보다 커지는 것을 수식으로서도 확인할 수 있으며 이과정을 통해 optimal한 value function에 도달할 수 있음을 알 수 있다.
3. GLIE
- ε-greedy 방식은 학습이 상당히 진행된 상황에서도 ε의 확률로 임의의 행동을 하게된다는 단점이 있다. 이 때 ε 값을 학습이 진행될수록 줄여준다면 무한히 학습이 되었을 때에는 greedy policy로 변하게 될 것이다.

- 이러한 조건을 Greedy in the Limit with Infinite Exploration (GLIE) 라고 부르며 위와 같이 두 가지 조건을 만족할 때 GLIE라고 정의할 수 있다.
Reference
[1]: Reinforcement learning: an introduction
[2]: Fundamental of Reinforcement Learning
[3]: Fast Campus 강의자료
[4]: Silver 교수님 강의자료
댓글남기기