Temporal Difference

ML study > Reinforcement Learning > Temporal Difference

1. Temporal Difference

• 앞서 살펴본 DP는 현재값으로부터 모르는 값을 추정하며 계산량을 줄이는 것이 가능했으나 환경에 대한 모델이 필요했다. 반면 MC는 sampling 방식으로 환경에 대한 정보 없이도 추정이 가능하지만 episode가 끝나야지만 value에 대한 update가 가능한 방식이었다.

• Temporal Difference 방식은 이 두가지 방식의 장점을 결합한 방법이라고 할 수 있다.

Source

• MC의 경우 episode 가 끝난 실제 return 값 (Gt)를 가지고 value function을 update 했지만 TD는 원하는 step 만큼의 reward를 얻고 그 이후는 estimated 된 값을 사용하여 return을 예측하고 이 값을 update 식에 사용하는 방식이다.

2. MC Control

• MC 에서도 DP와 마찬가지로 policy를 control을 greedy한 value function을 가지는 policy로 improve 한다고 가정하면 새로운 policy는 위와 같이 구해질 것이다. 이 때 value function을 가지고 새로운 policy를 구하게 되면 model의 환경을 알아야하기 때문에 MC의 control 문제는 evaluation과정을 통해 구한 행동가치함수를 사용하게 된다.

• 하지만 모든 table에 대해 계산하며 iteration을 거쳤던 DP와는 달리 MC는 일부분에 대해서 update가 되기 때문에 policy 를 improve 할 때 무조건 greedy한 policy를 선택하게 된다면 문제가 될 수도 있다. 실제로 다른 행동을 했을 때 더 좋은 return 값을 가질 수 있기 때문이다.

• 따라서 MC control에서 정책 π는 행동가치함수에 대하여 무조건 greedy한 action을 취하는 것이 아니라 ε의 확률로는 모든 가능한 행동 중 하나를 임의로 선택하도록 하는 ε-greedy 방식을 통해 policy control 문제를 해결할 수 있다.

• 직관적으로 ε-greedy 방식이 정책개선을 이루어낼 수 있다는 것을 보았지만 수식적으로도 확인이 가능하다.

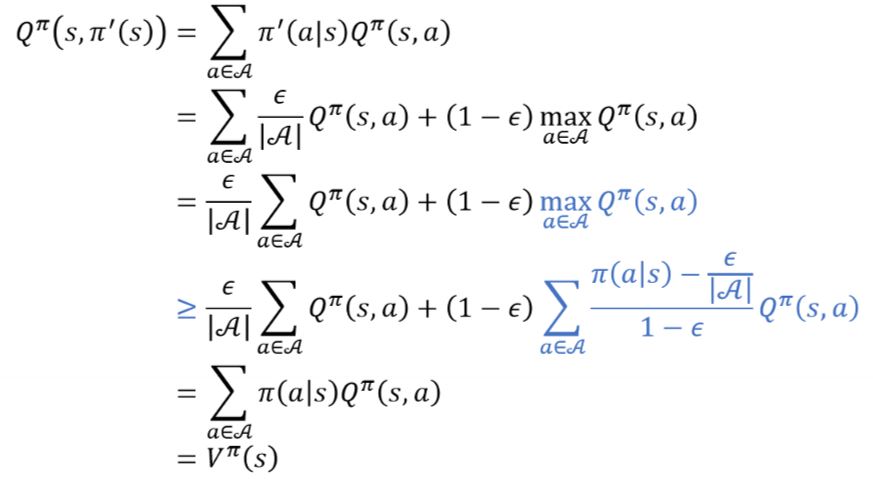
• 개선된 정책으로 부터 나오는 Q함수를 풀어서 적으면 위와 같이 차례로 유도가 가능하다.

• 이 때 3번째에서 4번째줄로 넘어갈 때, 파란색으로 칠한 부분이 한번에 이해가 어려울 수 있다. 4번째 나오는 시그마 term을 합하면 결국 1이 된다는 것은 알 수 있는데 이 값이 Q함수와 곱해져서 더한 값은 결국 Q함수의 max 값보다는 같거나 작을 수 밖에 없다. 따라서 3번째에서 4번째 줄로 넘어가게 되며 이후는 계산 및 정의를 통해 넘어갈 수 있다.

• 즉, Vπ’ 값은 Vπ보다 커지는 것을 수식으로서도 확인할 수 있으며 이과정을 통해 optimal한 value function에 도달할 수 있음을 알 수 있다.

3. GLIE

• ε-greedy 방식은 학습이 상당히 진행된 상황에서도 ε의 확률로 임의의 행동을 하게된다는 단점이 있다. 이 때 ε 값을 학습이 진행될수록 줄여준다면 무한히 학습이 되었을 때에는 greedy policy로 변하게 될 것이다.

Source

• 이러한 조건을 Greedy in the Limit with Infinite Exploration (GLIE) 라고 부르며 위와 같이 두 가지 조건을 만족할 때 GLIE라고 정의할 수 있다.

Reference

[1]: Reinforcement learning: an introduction

[2]: Fundamental of Reinforcement Learning

[3]: Fast Campus 강의자료

[4]: Silver 교수님 강의자료