MDP

ML study > Reinforcement Learning > MDP

1. 강화학습 문제정의

먼저 단 한 번의 선택만 하는 문제가 있다고 하자. 예를 들어 오늘 점심을 어디에서 먹을지, 어느 회사에 지원을 할지 결정하는 문제의 경우 한 번의 선택으로 끝이 난다. 이러한 문제를 One shot decision problem 이라고 하며 에이전트가 내리는 결정이 에이전트의 다음 판단에 영향을 주지 않기 때문에 classification 이나 regression과 같은 supervised learning으로 학습하는 것이 효율적일 것이다.

반면 회사에서 운전을 해서 집까지 가는 과정을 살펴보자. 운전자는 신호, 차선, 속도, 다른 차들의 위치 등을 고려해서 핸들의 각도, 기어, 액셀 등을 조정한다. 이것은 다시 신호, 차선, 속도 등의 상태에 영향을 끼치게 되고 그 상황에서 다시 행동을 결정하는 과정이 반복된다. 이러한 문제를 Sequential decision problem 이라고 부른다.

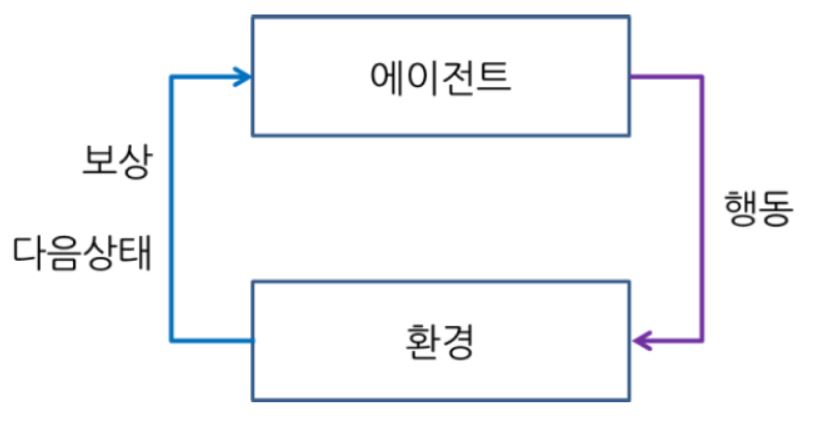
Sequential decision problem 에서는 정답이 존재하지 않기 때문에 supervised learning을 하기에는 적합하지 않다. 대신 에이전트와 환경이 상호작용을 할 때마다 reward (보상) 라는 것을 주게 되면 학습이 이루어 질 수 있으며 이러한 문제에는 강화학습을 적용하여 문제를 푸는 것이 적절하다고 할 수 있다.

지금까지 강화학습의 직관적인 형태와 어떤 문제에 대해서 적용하면 좋을지에 대해 살펴보았다. 이제는 강화학습을 수학적으로 정의를 해 볼 것이다. 결론부터 이야기 하자면 강화학습은 5가지 tuple로 이루어진 (S, A, R, P, γ) MDP로 정의가 되는데 이것이 무엇을 의미하는지 차근차근 알아볼 것이다.

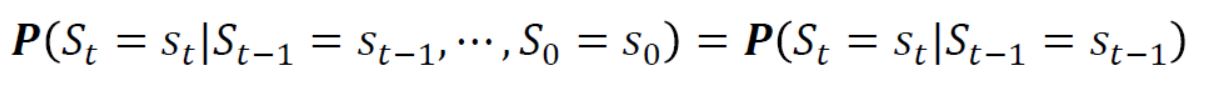
강화학습을 수학적으로 정의하기에 앞서 markov property 라는 것에 대해 먼저 알아야한다. 위 수식을 만족할 때 markov하다 혹은 markov property를 가진다 라고 하며 수식을 해석하면 처음 state 부터 직전 state 까지 고려하여 현재 state가 될 확률과 직전 state 만을 고려했을 때 현재 state가 될 확률이 동일하다는 뜻이다. 즉, Markov Property란 현재 상태는 오직 바로 이전의 상태로만 결정되는 특성을 말한다.

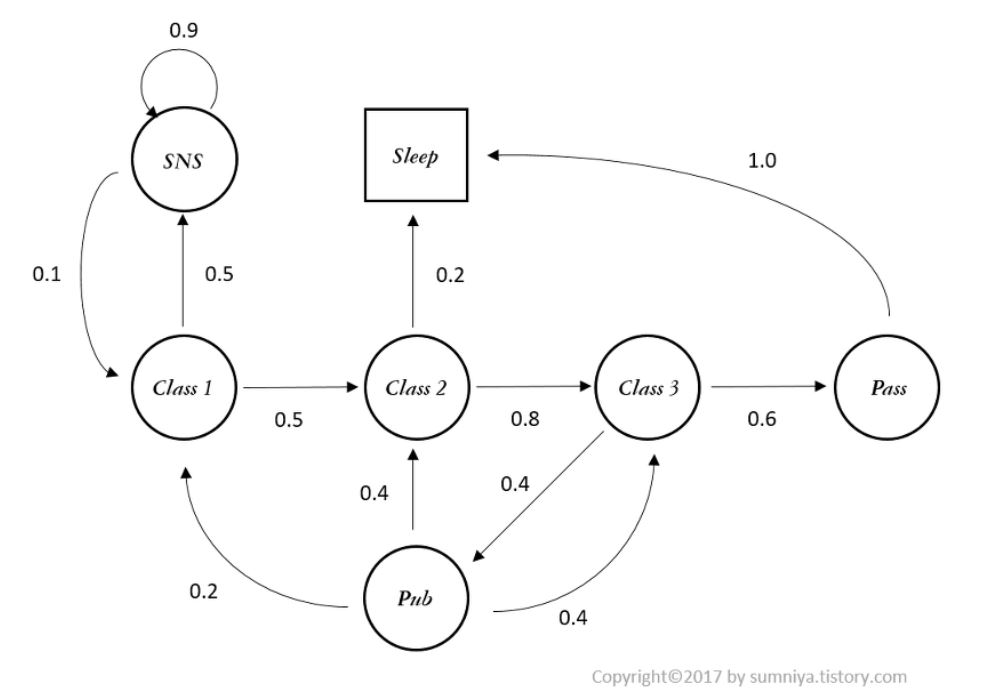
State가 markov 할 때, state 마다 정의된 상태변환확률에 따라 state끼리 이동이 일어나는 과정을 Markov Process (MP) 라고 한다. 즉 MP 는 상태와 상태변환확률로 구성된 (S, P) 의 tuple로 표현이 가능하며 위의 그림이 Markov Process에 대한 예를 도식화한 것이다.

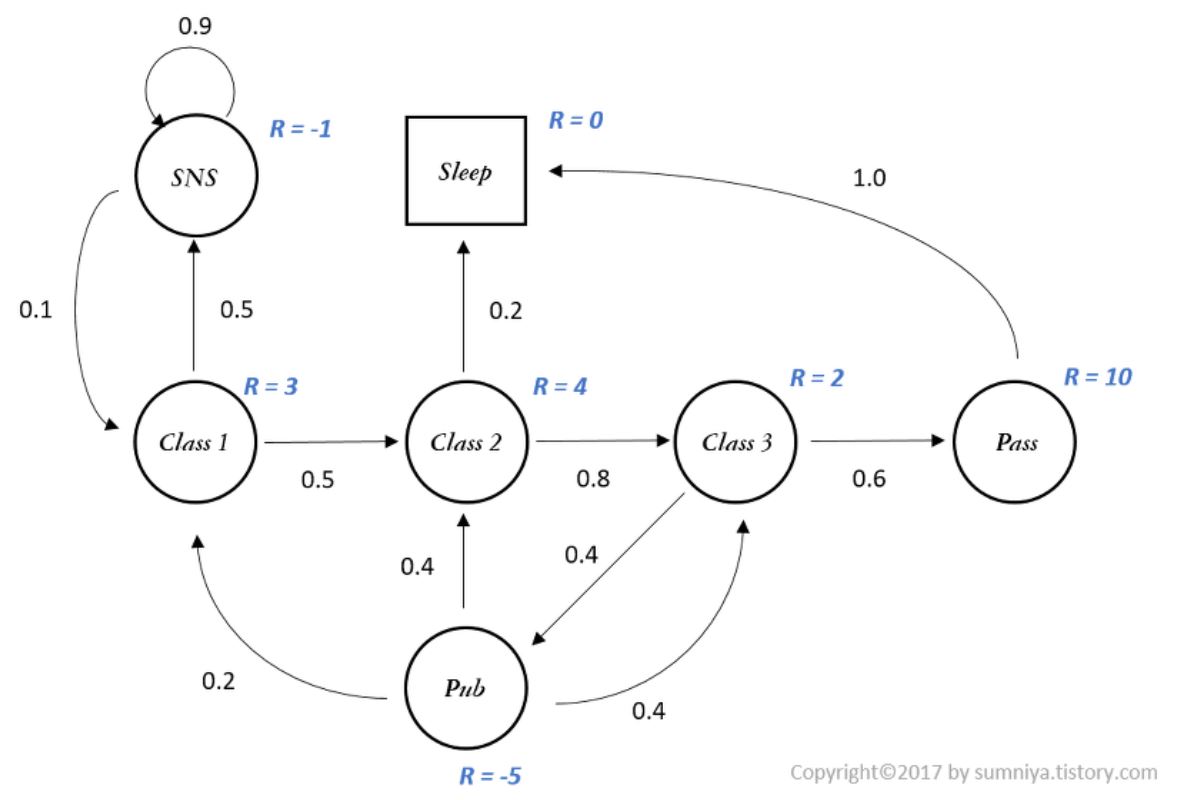
앞서 살펴본 MP 에서 state가 변환될 때 reward를 받는다고 환경이 있다고 한다면 이 과정은 Markov Reward Process (MRP) 라고 부른다. MRP는 상태, 상태변환확률, 보상, 감가율로 구성된 (S, P, R, γ) 의 tuple로 표현이 가능하다. 위의 그림은 MRP 과정의 예시를 나타낸 것이다.
감가율이라는 개념이 추가되었는데 이것은 현재 받는 reward보다 먼 미래에 받은 reward는 1과 0사이의 값을 곱해 현재가치로 변환히켜주는 역할을 해준다. 또한 state의 길이가 매우 길어지는 경우 감가율이 없다면 reward의 합이 무한대로 가버릴 수 있는 문제를 방지해 줄 수 있는 중요한 역할을 하는 요소이다.

마지막으로 살펴볼 Markov Decision Process (MDP) 는 MRP 에서 Action의 개념이 추가된 것이다. 앞선 process에서 state가 변환될 때는 단순히 상태변환확률에 의해서 변환되었지만 이제는 agent가 다른 state로 가기 위한 action을 하고 그 이후 상태변환확률에 의해 그 다음 state로 이동을 하게 된다. 즉, MDP란 상태, 행동, 상태변환확률, 보상, 감가율로 구성된 (S, A, P, R, γ) 의 tuple로 표현이 가능하다.
바로 이 MDP라는 과정이 Sequential Decision Problem, 즉 강화학습 문제를 수학적으로 표현한 것이라 할 수 있다.
이 때, MDP에 해당하는 정보를 모두 알고 있다면 우리는 state에서 최고의 가치를 가지는 action들을 Dynamic programming 이라는 방식으로 계산할 수 있다.
반면 이 상태변환확률을 모르는 경우 강화학습을 통해 reward로 부터 최적의 action을 할 수 있도록 학습이 가능하다.
다음 장에서는 정의한 강화학습 문제로 부터 어떻게 최적의 정책을 구할 수 있는지 살퍄볼 것이다.